一维差分

题目描述

输入一个长度为n的整数序列。
接下来输入m个操作，每个操作包含三个整数l,r,c，表示将序列中$[l, r]$之间的每个数加上c.
请你输出进行完所有操作后的序列。

输入格式
第一行包含两个整数n和m。
第二行包含n个整数，表示整数序列。
接下来m行，每行包含三个整数l，r，c，表示一个操作。

输出格式
共一行，包含n个整数，表示最终序列

数据范围
$1<=n,m<=100000$

$1<=l<=r<=n$

$-1000<=c<=1000$

$-1000<=$数列中元素的值$<=1000$

题目分析

差分就是将数列中的每一项与前一项数做差

通过构造差分序列的方式计算，这儿同样用一个示例图来帮助理解

代码实现

#include<bits/stdc++.h>
using namespace std;

const int N = 100010;

int a[N], b[N];
int main(){
    int n, m;
    cin >> n >> m;
    // 输入整数序列
    for(int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    // 初始化差分序列
    for(int i = 1; i <= n; i++)
        b[i] = a[i] - a[i - 1];
    
    // 一次输入询问
    while(m -- ){
        int l, r ,c;
        cin >> l >> r >> c;
        b[l] += c;
        b[r + 1] -= c;
    }
    
    // 还原前缀和得计算后的原整数序列
    for(int i = 1; i <= n; i++)
        b[i] += b[i - 1];
        
    // 输出整数序列
    for(int i = 1; i <= n; i++)
        printf("%d ", b[i]);
        
        return 0;
}

运行结果

输入

6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1

输出

3
10
14

总结

求差分，即是前缀和的逆向思维。

差分的性质：

1、差分序列求前缀和可得原序列

2、将原序列区间[L,R]中的元素全部+1，可以转化操作为差分序列L处+1，R+1处-1

3、按照性质2得到，每次修改原序列一个区间+1，那么每次差分序列修改处增加的和减少的相同

二维差分

题目描述

输入一个n行m列的整数矩阵，再输入q个操作，每个操作包含五个整数$x1,y1,x2,y2,c$，其中$(x1,y1)$和$(x2,y2)$表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上$c$。
请你将进往完所有操作后的矩阵输出。

输入格式
第一行包含整数n,m,q。
接下来n行，每行包含m个整数，表示整数矩阵。
接下来q行，每行包含5个整数x1,y1,x2,y2,c，表示一个操作。

输出格式
共n行，每行m个整数，表示所有操作进行完毕后的最终矩阵。

数据范围
$1<=n,m<=1000$

$1<=q<=100000$

$1<=x_1<=x_2<=n$

$1<=y_1<=y_2<=m$

$-1000<=$矩阵内元素的值$<=1000$

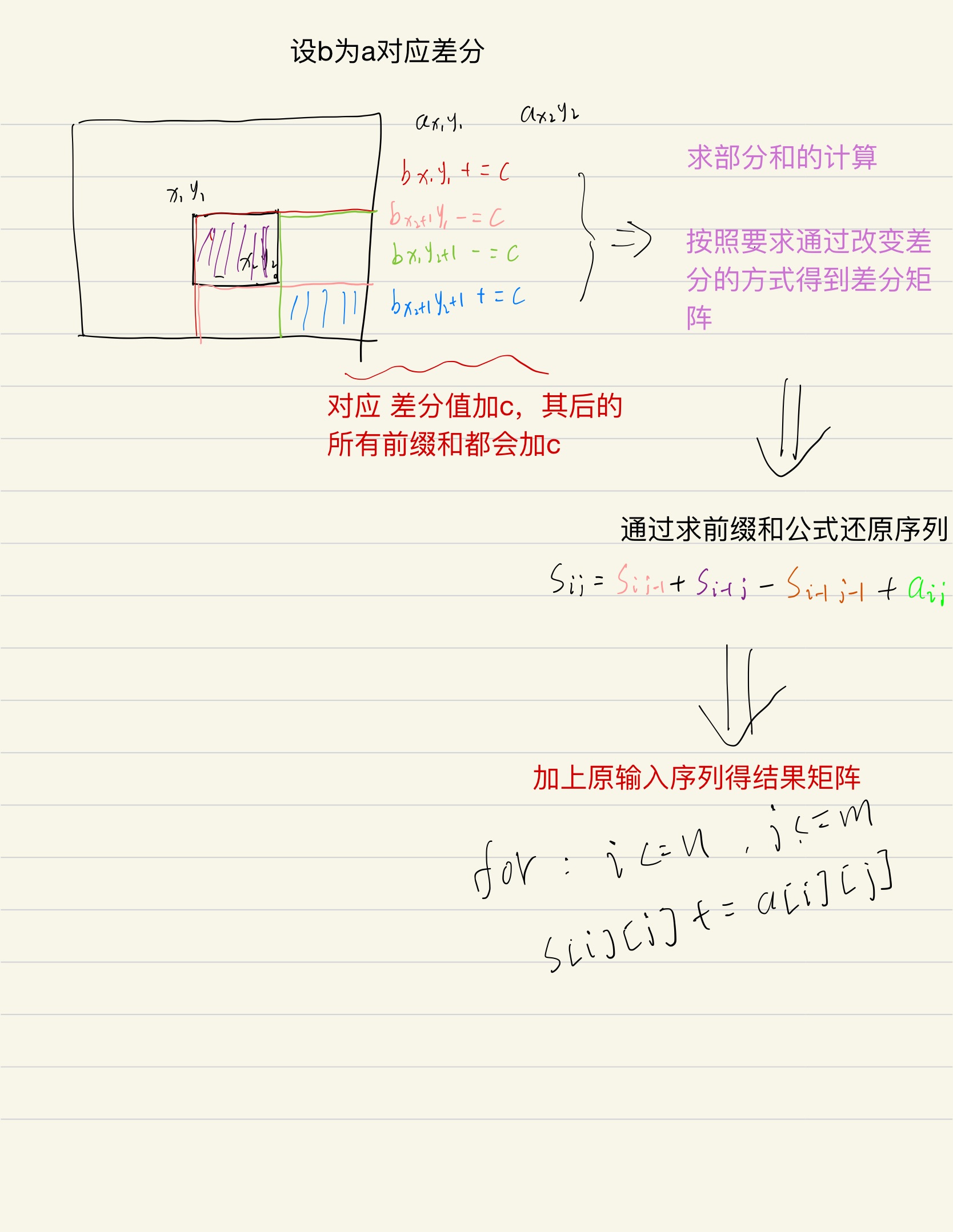
题目分析

代码实现

#include<bits/stdc++.h>

using namespace std;
const int N = 1010;

int n, m, q;
int a[N][N], b[N][N], s[N][N];

// 初始化差分矩阵
void insert(int x1, int y1, int x2, int y2, int c){
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

int main(){
    // 分别输入序列长度n 与 访问次数 m
    scanf("%d %d %d", &n, &m, &q);
    // 输入整数矩阵
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            scanf("%d", &a[i][j]);

    // 依次询问
    while(q --){
        int x1, y1, x2, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        // 计算对应 + c 差分值
        insert(x1, y1, x2, y2, c);
    }

    // 还原二维前缀和得原序列
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + b[i][j];

    
    // 加上原本输入的原整数矩阵
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= m; j++)
            printf("%d ", s[i][j] + a[i][j]);
        printf("\n");
    }

    return 0;
    
}

运行结果

输入

输出

2 3 4 1
4 3 4 1
2 2 2 2

总结

儿